
Finally got my act together and did a semi-proper, 3-part, problem-based learning lesson today in math!
We began with a hundreds chart warm up (the students are becoming increasingly proficient at noticing and describing patterns, using mathematical language), then got them busy with the whiteboards solving the problem. They could choose to work alone, or with a partner, and could use any strategies they wanted to solve the problem. (I reminded them of the 4-part problem solving model we had looked at the other day, and also referred them back to the chart we had begun to make listing various strategies.)
It was reaffirming to see how students used a variety of methods to arrive at the same solution (i.e. that each row of tiles in the pattern was shrinking by 2)… some used a table and noticed the pattern, others recreated the pattern with colour tiles, and continued it until they got the answer they needed (one boy did this using the “infinite cloners” I had created on the smart board), still others drew a picture to illustrate the problem, and that seemed to help them figure out the subsequent rows and numbers of tiles.
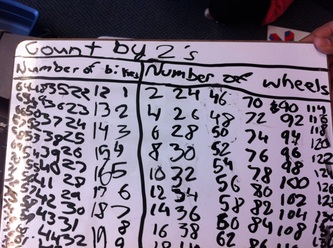
Interestingly, one student drew a very detailed photo of a bicycle from Friday’s problem, apparently completely missing the point I had made earlier about details being great for Art or Science, but not so necessary in a sketch for math!
(bicycle problem solutions from Sept 21)

At the end of the lesson, a number of students came up and shared their responses using the document camera; I took a photo of their solutions and posted them on the smart board, annotating the solution with a coloured Smart pen as the student(s) spoke.
After each solution shared, I made it small and moved it off to the side, so that we could still refer back to it as the next student shared his/her solution on the board.
Although I am pleased with the capabilities of the Board for conducting such a lesson, I have ongoing concerns about the students who don’t seem to “get it”. Some of the children seem so far behind in math – even with 1:1 guidance from our in-school support person, they were struggling to understand the problem, let alone consider how it might be solved… and the debrief part of the lesson, where the “math teaching” comes to the forefront, these same students either struggled to pay attention to the student presenting a solution and barely focused on my “teaching” through the solution, or they simply checked out altogether, and simply played with their colour tiles or drew on their whiteboards while their peers engaged in academic dialogue.
How to draw these learners into the conversation – while still maintaining a pace and interest level appropriate to the learners ready for the next challenge – will be my ongoing experiment this year!







 RSS Feed
RSS Feed