No matter where they were when they started, every student who agreed to have their work photographed ended up with a Level 3 or 4 answer. My goal was to make every child feel like they could achieve at or above standard, by showing them how small tweaks to what they'd already written could dramatically improve their communication.
|
As EQAO approaches, we've spent some time comparing our written responses to various open questions to exemplars from the EQAO website, using student responses from previous years as anchors, and then considering how to improve our responses.
No matter where they were when they started, every student who agreed to have their work photographed ended up with a Level 3 or 4 answer. My goal was to make every child feel like they could achieve at or above standard, by showing them how small tweaks to what they'd already written could dramatically improve their communication.
0 Comments
Today guest blog is written by Jason Rodger, a CCT and Grade 6 MFI Teacher in Ottawa, Ontario. If you like what you read below, or even if you want to challenge it, please post a comment. I will be interviewing Jason and his colleague, Michael Wendler, this Friday, to talk about Interactive White Boards and Math. Your comments will help engage the conversation. So please, consider leaving a comment below, or contact me here.
I remember in my first year of teaching, looking around my empty classroom, bereft of resources and manipulatives, and seeing textbooks galore, thinking: There has to be a better way. It struck me finally one day when one of my students asked me about the question in the text. “Do farmers really count kernels of corn?” If I was going to teach math I was going to have to teach it differently. I needed to teach math in a way that made sense to me and was going to contribute to my students learning in a more meaningful way. Within a week, I had rolled an unused media cart into my classroom, I had commandeered the little-used computer lab across the hall, and the textbooks were ditched. I was all-in and extremely nervous that -- as a new teacher -- I was going to be “found out” and my choices would be questioned. Six years later and the books have never made their way back in. So how, as a new teacher, or one wishing to make the transition, do you begin a technology based math program? Read, Read and Read Some More There are some amazing digital resources available to teachers, and Twitter has become my chief source of education and technology news. Create your own network of educators and begin to read what they post. Begin following the people whom they follow. Find your board’s technology and math gurus, and ask them to point you in the right direction. My go-to site for tech education is Clif Mims, member of the University of Memphis‘ Instructional Design and Technology faculty since 2005. His news daily can be read here: http://paper.li/clifmims/1334294157 Become the Tech Expert I hear from a lot of teachers that they don’t have any technology at their disposal. Does someone else at your school? A friend at another school? Can you register for workshops which would be of interest? You must invest the time in learning the technology. Simple as that. You cannot expect to use technology as a part of your daily math lessons if you have never explored the technology yourself. In using the technology you will naturally think of new and interesting ways of using it as a part of your math program and develop ways to integrate it into the curriculum. Always remember that the curriculum tells us what to teach but not how to teach it. Here are some links to get you started: 3D Tin: www.3Dtin.com Google SketchUp http://www.sketchup.com/intl/en/ The National Library of Virtual Manipulatives http://nlvm.usu.edu/en/nav/vlibrary.html The Medium is Not the Message Technology is cool. Technology is fun. It is also expensive. The novelty of using technology in the classroom is fleeting. When I began using technology to teach math six years ago, technology had not yet penetrated every aspect of our lives; using technology was enough to captivate students' attention and hold it. No more. Technology in the math classroom has to have a purpose. I hear teachers say it would be neat to have X piece of technology in their room. If it’s neat you are looking for, look elsewhere. These are tools that can be used to create amazing work, whether 3D landscapes and architecture or using an excel spreadsheet to graph student generated survey results. If students are given real work, with a true purpose, incorporating newly acquired tech skills, they will surely fly. Still not Convinced? Here are a couple of inspirations for you. The first is a very well known RSA talk by Sir Ken Robinson about the need to change the delivery of education, and a new talk about education’s Death Valley The second is a TED talk by British technologist and big thinker Conrad Wolfram. He advocates strongly for introducing tech into maths and makes a compelling argument. Start with integrating one new item a month to your teaching and before you know, it you’ll be an expert spreading the gospel of tech to your colleagues! Jason Rodger is a CCT and Grade 6 MFI Teacher in Ottawa, Ontario. He and his colleague, Michael Wendler, will be interviewed by me on Skype this Friday, May 17, 2013. Please leave a comment or question which you may want him to address during our interview later this week. Interview blog will be posted next week.  Probability comprises concepts that many adults struggle to understand. (Not convinced? Just have a look at our booming lottery business!) How, then, can we engage children in such a way that ensures they build a solid foundational understanding of this important mathematical area? Since many of my students have developed strong oral language skills this year, especially when working with a partner or in a very small group, I developed a series of lessons that drew heavily on the instructional strategy of "think-pair-share", and banked on Van De Walle's games-rich chapter on probability. We spun spinners, rolled dice, made and tested predictions, played "hockey" and other goal-based games that depended on predicting outcomes. But first, we explored the basic vocabulary of probability: chance, possible, certain, impossible, likely, unlikely, equally likely.... A number of scenarios were presented on the board, and students had to discuss whether each was certain, possible, or impossible. Then we moved each scenario into the appropriate part of a Venn diagram on the Interactive White Board. Lots of wait time was provided for students to consider and discuss each scenario, and as you can see from the photo above, they were quite engaged: For once, every student was either looking at the screen, or discussing the scenario with nearby neighbours!  Next, students engaged in a "continuum of probability" mini-lesson, in which we moved a series of five different spinners into sequence from impossible to certain. It was a great opportunity for them to see each of the new words they had learned in the bigger context of probability vocabulary and concepts. Finally, after lots and lots of thinking and rich talk, I asked students to work on their own to write down a few examples of things that were likely, impossible, certain, etc. I used this exit ticket as a diagnostic assessment to see what level of understanding most of the learners were at in order to fine tune my next lesson, which involved a series of probability math games. Yes, we went to the conference. Yes, it was awesome. Yes, I learned a lot. Yes, I will blog about it... soon... cut me some slack: My dawg died last week, and I'm trying finish up some probability lesson problems (on my own time; we're out of release days; Ack!), and it's 7 p.m., and I'm still in my classroom and haven't had dinner, lol!
Stay tuned... Communication. It’s an essential component of mathematics, especially when dealing with a student population whose first language is NOT the language of instruction! A few weeks ago, I wrote about the simplification of criteria in order to help focus students on writing clear and succinct explanations when communicating solutions to problems they solve. That strategy seems to have worked for many of the students in my class: Below is a sample from some multiplication/division problems they solved the other day. As one can see, it is easy to assess their understanding of the concept, as well as note where errors were made (and by following up with a short conference, one can surmise if those errors were mathematical, or linked to a misreading of the problem itself, due possibly to ESL factors). Speaking of conferencing, my colleague, Dale, recently reminded me of the value of this: As we finished up our transformational geometry unit a few weeks back, he elected to evaluate students by meeting with them individually to orally assess their understanding of transformation understanding. Dale showed what he had students do, including a question or to using a grid map from the text book, and a few tasks involving the translation, reflection and rotation of an object on a grid paper. For each task, he made note of whether they were able to do it independently and confidently, whether they benefited from some teacher guidance, or whether they seemed completely at a loss, even with teacher intervention and support. (I stole his idea and created a recording template -- see photo below.) In some sense, the conference became a bit of a teaching opportunity as well as an assessment measure. We conference daily or weekly with students for reading and writing as a way to assess and remediate as needed, why not in Math?!  I've often harped on the importance of employing "talk before writing" strategies like "think-pair-share"... Another thing I’ve noticed, both while conferencing AND while using such instructional tactics as “think-pair-share”, is the importance of wait time. It can take a while for students to focus and get on-topic. Giving them a few extra seconds or even minutes to chat with a partner, instead of rushing them through a discussion topic, can really help students to go a little deeper with their understanding. Although I know the research on wait time, I am always surprised when I actually remember to use it, and then students' responses are richer and more focused! Simplifying success criteria, using oral conferencing as a form of assessment and integrating wait time into the instructional repertoire... three of the many ways we can increase student success as they communicate in math. In the final months of school, we'll be reflecting more on the original goals of the project, and assessing the overall impact of this project on both student learning and teacher practice. We'd love to hear from some of our blog followers so that we can assess the real impact (if any) on the audience outside our classroom!
Please, consider commenting on one or more of our blog posts, take our polls, or drop us a line by email. Don't be shy, be honest! We want to hear the good, the bad and the ugly. How did you find this website? How have you used our site, and in what ways has it been helpful, contentious or useless? Was there something you wished there had been more of? Less of? Your feedback will help us to make our final report to the ministry come alive!!  Finally finished our Fractions unit... As our release days are dwindling, this time we cranked out four lessons throughout the day at lunch and after school as able, rather than during a release day. I found it rather a challenge to "get into" the math planning frame of mind for a short time and then be forced to leave the work session -- often mid-lesson -- and move on to something else (like teaching our classes, running out to do yard duty, or leaving school to go home and make dinner for my own kids!!), but it was an important experience for us to remember what it is like for the average teacher, who doesn't have a bunch of release days specifically for planning purposes. Using Vandewalle as our philosophical guide, we consulted the curriculum to ensure we stayed focussed on what was actually being asked of grade threes, then set forth to plan a series of lessons that would introduce students to and engage them with halves, quarters, sixths and other fractions. Knowing from Ministry of Ed findings a few years back that fractions are a part of the math curriculum that seem to cause some students grief and heartache, we made sure to include problems from all three perspectives: area, linear and set models. We hope you enjoy this series of lessons (scroll down to the bottom of that page). Our next and final Smart Bansho unit will be "Probability", and it will hopefully be complete and uploaded by the end of the month. Thanks to all who have been using or experimenting with our lessons. Please feel free to leave comments or drop us a line with any feedback. As my students were working on a problem the other day, I wandered around to video tape them, just to get a sense of how things work in my classroom during the "action" phase of a lesson. I caught a few students' explanations of their solutions on camera, then turned the camera off.
No sooner had a turned off the camera, then an intellectual debate broke out amongst four students -- I quickly turned the video camera back on, and caught the tail end of the argument. At issue was the number of crossings a ferry captain has to make to get from one side of the water to the other in order to ferry a total of 26 cars across from the mainland to the airport where Ms. Teschow takes her flying lessons. (The ferry boat can hold a maximum of 8 cars per crossing.) The boy I had just been filming claimed it would take 8 crossings, however, the fellow in the zip up jacket with the orange collar claimed the number to be 7. In the snippet below, he attempts to show why. (Note that although he struggles with clearly articulating his thinking, everyone is very polite, even when they animatedly disagree. Note also zip-up guy's "patterned" diagram on his whiteboard, which we later shared in stages with the rest of the class.) I am so tired of students writing and writing and writing around in circles, and not actually SAYING anything, when it comes to "explaining their thinking" in math! There are a tonne of words on the page, and sometimes even elaborate pictures with intricate details, but the mathematical communication is weak at best. Certainly, few teachers or other students could look at the so-called solution and make out what exactly the students did. As I have been reflecting on this in recent weeks, it occurs to me that perhaps our criteria are too many and too specific. Today, we summarized the long list we had made several weeks ago, and re-wrote our criteria list. On it now were only two items: 1. Write a sentence that answers the question. 2. Show how you got the answer. We began with a problem as usual, and then, after the debrief, I transferred the solutions we had collectively come up with to an anchor chart, under the heading, "Does your solution show what you did to get the answer? Can we see how you solved the problem?" Since there were four different examples given, students could see that there is more than one way to do this. We also noted that it was important to remember to include an actual sentence that answers the question. Some students had been getting so caught up in the solution, that they never actually answered the question. Insisting that they do so helped many of them clarify their own understanding of what it was they were thinking about. This lesson was only one example of the effectiveness of the new, shorter and hopefully improved criteria list; stay tuned for the long-term test of its value.
 It's easy to get discouraged when biting off a big chunk of something new. I often wonder whether -- with this new way of doing business in my math classroom -- my students are even learning anything, not just about the specific curriculum expectations, but about the processes and general culture of mathematics. Do they see themselves as mathematicians-in-training? Are they becoming thinkers? Problem solvers? Are they having FUN in math, even if it is hard for them to understand some of what we are doing? Are they seeing the tremendous beauty of the order and innate design in mathematics? My principal happened to walk into my classroom the other day, when it was all humming along nicely: I was lying on the carpet, working with a small group of students on a multiplication/division problem. Several other students were scattered around the room, working alone or in pairs on the same problem or a variation thereof. Children were wandering by every now and again, helping themselves to whatever manipulatives they needed from the math bins, to help them think through and solve the problem. One student was curled up on the couch, reading a math dictionary. A Spec Ed/ESL teacher sat at a table nearby, working with a small group. One child was using a clock at the back table, along with some flash cards she had made to test herself ("time" was something she had been struggling with in recent weeks, and she was determined to master it). Truly, it was the text book picture of Differentiation! But it isn't always like that. And even when it is, it can feel like just a drop in the bucket, in terms of the many learning needs that need to be met with my incredibly diverse classroom population.
Sometimes I question myself about whether I am even making a difference for these students. Last night, though, I had an experience that suggests that I am making a difference... I was "field testing" some math lessons with my own two kids at home; they happen to also be in Grade 3 this year. I showed them the warm-up questions, and we used pattern blocks to do it together, before I set them loose with the actual problem. "This is fun, Mommy!", exclaimed one of my children, suggesting that he rarely participates in this sort of problem-based approach to learning. (The pages and pages and pages of math worksheets that come home in his backpack further support this inference.) "We don't have those colour blocks, only for EQAO", noted his twin brother. WOW! Seriously? The poor child didn't even know the name for pattern blocks. I asked if they had access to math manipulatives in their classroom. In general, they did not seem to. Both boys said that the teacher sometimes let them use them for a certain question, or during "EQAO practice", but neither knew where the manipulatives were kept in the classroom, if there were any in the classroom. Kind of scary, I thought. Imagine if one didn't know where the books were, for reading. How is it okay, in this day and age, to not expose children to and encourage their use of a WIDE variety math manipulatives?! In my opinion (and, I might add, the opinion of the MInistry of Ed, based on years of extensive research), children should be able to come and go and freely help themselves to the learning tools they need when working through a problem. To deny them access to, or to decide FOR them, which learning tools they will use is to deny them the opportunity to think, construct and grow in their understanding of a mathematical concept. So, I pride myself that the students in my classroom know the names for and can use a variety of math manipulatives. They are still learning -- in some cases -- how to use them effectively, but they are not afraid of interacting with them, not as toys brought out on a special occasion, but as powerful thinking tools to aid in their understanding of mathematics. |
AuthorVera C. Teschow is a teacher, vegetarian, student pilot, drummer, and mother of monozygotic twin boys. Archives
June 2013
|








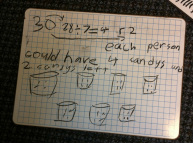






 RSS Feed
RSS Feed